Table of Contents
Introduction: The New Era of Quantum Computing and Information Reality
Classical computers have carried us far. They transformed society, connected billions of people, and solved problems once thought impossible. Yet they face clear limits. At the heart of classical computing lies the logic gate, a device that processes bits strictly as zero or one. These logic gates are arranged into circuits that evaluate instructions step by step. When problems grow large, such as simulating molecules or optimizing vast networks, classical circuits must test possibilities sequentially or with limited parallelism, which quickly becomes inefficient.
Quantum computing changes this foundation. Instead of logic gates acting on bits, it uses quantum gates that operate on qubits. A qubit is not confined to a single state. It can exist in a superposition, representing multiple possibilities at once. When several qubits interact, quantum gates create correlations that classical logic cannot reproduce. These gates are organized into a quantum circuit, where computation unfolds as a controlled evolution of quantum states rather than a chain of yes-or-no decisions.
In a quantum circuit, the computation behaves more like a wave than a checklist. Correct outcomes are strengthened, while incorrect ones interfere destructively. The challenge is practical, not conceptual. Qubits are fragile and easily disturbed by their environment. Still, steady progress suggests quantum circuits may soon complement classical systems, opening paths where logic gates alone cannot reach.
Quantum Computing Principles Overview
| Quantum Principle | Core Impact on Computing |
|---|---|
| Superposition | Enables qubits to explore multiple computational paths simultaneously rather than sequentially |
| Entanglement | Creates coordinated quantum states across qubits without classical communication channels |
| Interference | Amplifies probability of correct solutions while canceling incorrect computational paths |
| Quantum Tunneling | Allows systems to bypass energy barriers that trap classical optimization algorithms |
| Quantum Measurement | Collapses probabilistic states into definite outcomes governed by Heisenberg uncertainty |
| Error Correction | Protects quantum information from environmental noise through redundant encoding schemes |
1. Quantum Computing and Superposition: Expanding the Space of Possibility
A classical bit sits firmly in one state. It is either zero or one at any given moment. This definiteness makes classical computers predictable and reliable. It also constrains them. To evaluate multiple possibilities, a classical computer must check each one in sequence or use multiple processors running in parallel.
Superposition breaks this limitation. A qubit in superposition exists in a combination of zero and one states simultaneously. This is not ignorance about which state it occupies. Rather, the qubit genuinely participates in both states until measured. Two qubits in superposition can represent four states at once. Three qubits represent eight states. The pattern continues exponentially.
This scaling drives the potential power of Quantum Computing. With fifty qubits in superposition, a quantum computer can explore more than a quadrillion states simultaneously. A classical computer would need to examine each state separately, requiring astronomical time for certain problems. The quantum system processes all these possibilities together through its natural evolution.
Consider searching an unordered database. A classical computer must check entries one by one. Even with clever tricks, the time grows linearly with database size. A quantum computer using superposition can search the same database in time proportional to the square root of its size. For a million entries, this transforms a million steps into merely a thousand.
Yet superposition alone does not guarantee advantage. The quantum system must eventually produce an answer through measurement, which collapses the superposition. Without careful algorithmic design, measurement might return any of the explored states randomly, wasting the parallel exploration. The true power emerges when superposition combines with other quantum phenomena.
Quantum Computing Applications of Superposition
| Application Domain | How Superposition Enables Progress |
|---|---|
| Drug Discovery | Simultaneously explores molecular configurations to identify promising pharmaceutical compounds |
| Financial Modeling | Evaluates multiple market scenarios in parallel for improved risk assessment strategies |
| Cryptography | Tests many potential encryption keys at once in attacking classical security systems |
| Machine Learning | Processes training data through superposed states for pattern recognition acceleration |
| Weather Prediction | Models atmospheric conditions across simultaneous scenarios improving forecast accuracy |
| Materials Science | Simulates quantum properties of materials in superposition to discover new compounds |
2. Quantum Computing and Entanglement: Coordinated Information Beyond Distance
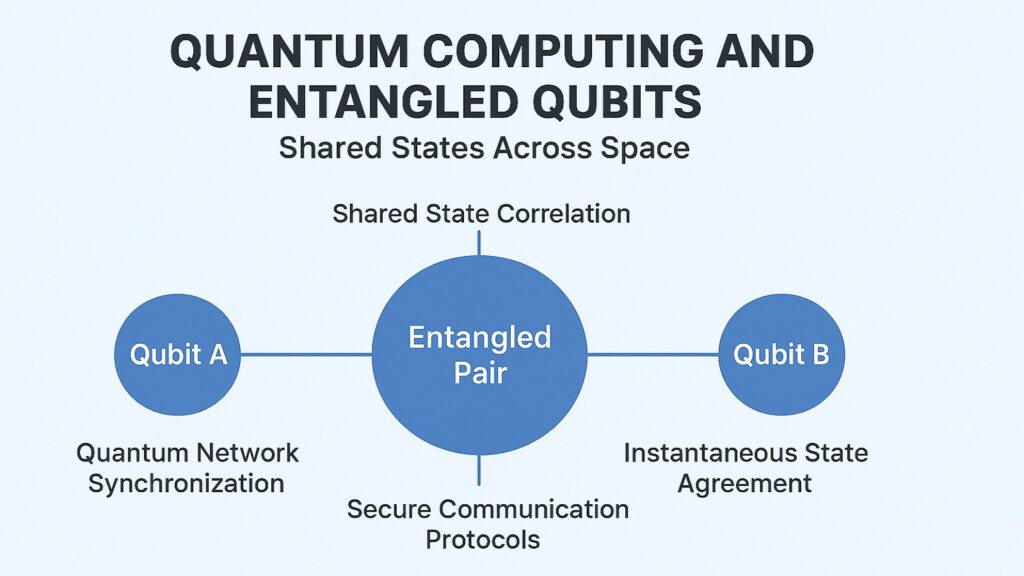
Einstein called it spooky action at a distance. He was troubled by entanglement, though experiments have since confirmed its reality. When two qubits become entangled, measuring one immediately determines the state of the other, regardless of the distance separating them. This correlation exceeds what classical physics allows.
Entanglement does not transmit information faster than light. Instead, it creates a shared quantum state between particles. Before measurement, neither qubit has a definite value. They exist in a combined state where their fates are linked. Once you measure one qubit and find it in state zero, the other qubit instantaneously settles into its correlated state. This happens not through any signal passing between them but because they share a single quantum description.
For Quantum Computing, entanglement provides coordination without communication. In classical parallel computing, separate processors must exchange messages to coordinate their work. This communication creates bottlenecks and limits scaling. Entangled qubits can perform coordinated operations without these classical channels. The correlation is built into their quantum state.
Quantum algorithms exploit entanglement to solve problems faster than classical approaches. When factoring large numbers, Shor’s algorithm uses entanglement to link the quantum state representing potential factors with the state representing their products. This correlation allows the algorithm to identify factors efficiently, threatening current encryption systems that rely on factoring’s difficulty.
Entanglement also enables quantum networks. Two parties can share entangled qubits and use them to establish provably secure communication channels. Any attempt to intercept the communication disturbs the entanglement, revealing the eavesdropping. China demonstrated this technology with quantum satellites, and research groups are building quantum internet prototypes.
Quantum Computing Benefits from Entanglement
| Technology Application | Role of Entanglement |
|---|---|
| Quantum Cryptography | Creates unhackable communication channels through shared entangled states |
| Distributed Computing | Links quantum processors across locations without classical data transmission |
| Quantum Sensors | Enhances measurement precision through correlations between entangled detector elements |
| Quantum Teleportation | Transfers quantum states between distant locations using entangled pairs |
| Quantum Algorithms | Enables computational speedup through coordinated quantum state evolution |
| Quantum Networks | Forms backbone infrastructure for future quantum internet connections |
3. Quantum Computing and Interference: Strengthening Right Answers, Canceling Wrong Ones
Superposition creates many possibilities. Entanglement coordinates them. Yet neither guarantees correct answers. The missing piece is interference, the phenomenon that makes Quantum Computing genuinely powerful rather than merely parallel.
Quantum states behave like waves. They have phases that can align or oppose each other. When two quantum waves with matching phases meet, they reinforce, growing stronger. When their phases oppose, they cancel, potentially disappearing entirely. This interference happens naturally as quantum systems evolve according to Schrodinger’s equation.
Quantum algorithms harness interference deliberately. They arrange computational steps so that correct answers accumulate through constructive interference while incorrect answers destroy each other through destructive interference. By measurement time, wrong paths have canceled out, leaving only the solution with high probability.
Grover’s search algorithm demonstrates this principle clearly. The algorithm works by repeatedly applying two operations. First, it flips the phase of the target item in the database. Second, it performs an inversion about the average amplitude. These steps gradually amplify the target while suppressing all other items. After roughly the square root of N iterations for a database of size N, the target state has a high probability, and others have been canceled.
Shor’s factoring algorithm uses interference even more subtly. It encodes potential factors in quantum superposition, then applies operations that create interference patterns related to the period of a mathematical function. Measuring this interference pattern reveals the period, from which the factors can be computed classically. The speedup comes from quantum interference,e extracting the period exponentially faster than classical methods.
Without interference, quantum computers would offer no advantage over classical randomized algorithms. Both could explore many possibilities, but neither would reliably find solutions. Interference transforms random exploration into directed search, making Quantum Computing fundamentally different from classical probability.
Quantum Computing Through Interference Mechanisms
| Algorithm Type | How Interference Creates Advantage |
|---|---|
| Search Algorithms | Amplifies target states while canceling non-target states through phase manipulation |
| Factoring Algorithms | Creates periodic interference patterns revealing mathematical structure of numbers |
| Optimization Algorithms | Guides system toward minimal energy states by suppressing high-energy paths |
| Simulation Algorithms | Maintains quantum coherence allowing accurate modeling of molecular dynamics |
| Machine Learning | Enhances pattern recognition by interfering training examples in quantum feature space |
| Sampling Algorithms | Generates probability distributions through interference of computational basis states |
4. Quantum Computing and Quantum Tunneling: Exploring Solutions Beyond Barriers
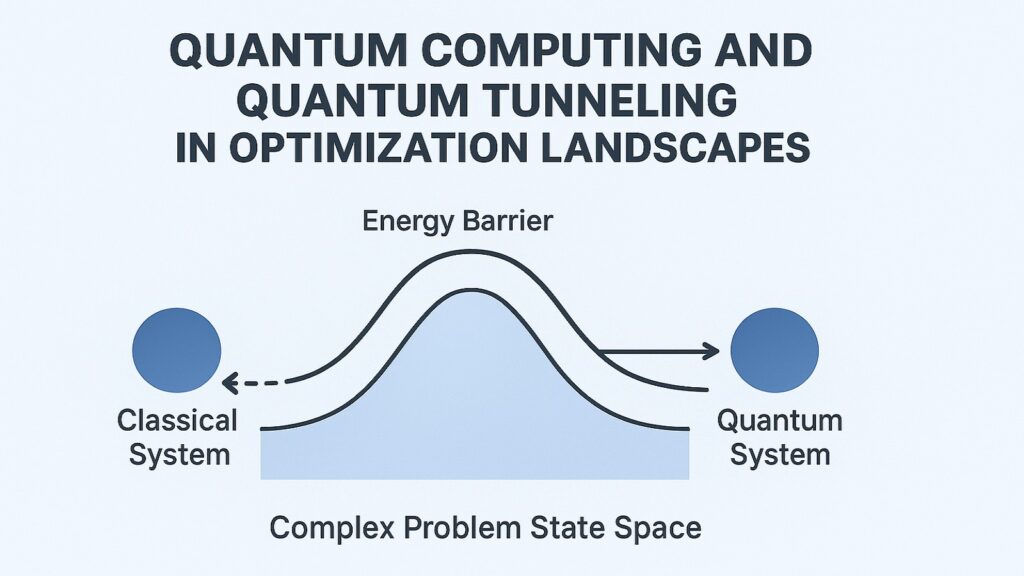
Classical optimization faces a persistent problem. Algorithms can get trapped in local minima, solutions that appear optimal locally but are inferior globally. Imagine climbing a mountain range in fog, trying to reach the highest peak. If you always step upward, you might reach a small hill’s summit and stop, unaware that a taller mountain lies beyond a valley.
Classical computers must either accept these local minima or invest enormous effort in systematically exploring all possibilities. For complex optimization problems with many variables, the solution landscape contains countless hills and valleys. Exhaustive search becomes impractical.
Quantum tunneling offers an alternative. In quantum mechanics, particles can pass through energy barriers rather than climbing over them. A ball thrown at a wall classically bounces back. A quantum particle has some probability of appearing on the other side without ever having enough energy to surmount the wall. This seems impossible from everyday experience, yet experiments confirm it routinely.
Quantum annealing exploits tunneling for optimization. The system begins in a superposition representing all possible solutions. It then slowly evolves, with quantum effects gradually diminishing. During this process, the system can tunnel through barriers separating different solution regions. As quantum effects fade, the system settles into a low-energy configuration corresponding to a good solution.
D-Wave Systems has built quantum annealers with thousands of qubits specifically for optimization. These machines have tackled problems in logistics, machine learning, and materials science. While debate continues about the extent of their advantage over classical methods, they demonstrate tunneling’s practical application.
Research suggests that quantum tunneling also plays role in biological processes. Some enzymes appear to use tunneling to transfer electrons or protons during chemical reactions. If biology harnesses quantum effects naturally, engineered quantum systems might enable new approaches to understanding and designing biochemical processes.
Quantum Computing Uses of Quantum Tunneling
| Problem Domain | Tunneling Contribution |
|---|---|
| Portfolio Optimization | Escapes local minima in financial asset allocation strategies |
| Traffic Flow | Finds globally efficient routing patterns by tunneling through barrier states |
| Protein Folding | Explores molecular configurations avoiding entrapment in metastable structures |
| Supply Chain | Optimizes logistics networks by bypassing locally optimal but globally poor solutions |
| Drug Design | Searches chemical space for molecules with desired properties across energy barriers |
| Machine Learning | Improves training of neural networks by escaping poor local optima |
5. Quantum Computing and Quantum Measurement: Understanding Through The Heisenberg Uncertainty Principle
Measurement seems straightforward in classical computing. You check a bit and find zero or one. The measurement does not change the bit. You can measure repeatedly and get the same answer every time. Classical information is robust and definite.
Quantum measurement operates differently. Before measurement, a qubit exists as a probability amplitude, a complex number encoding both the likelihood of different outcomes and their quantum phase relationships. This amplitude evolves smoothly according to quantum mechanics. Measurement disrupts this evolution, forcing the qubit to commit to either zero or one.
The Heisenberg Uncertainty Principle makes this disruption fundamental rather than technical. Heisenberg showed that certain pairs of quantum properties cannot both be known precisely. Position and momentum form one such pair. The more accurately you determine a particle’s position, the less you can know about its momentum, and vice versa. This is not about measurement tools being crude. It reflects deep quantum reality.
For qubits, uncertainty manifests differently but remains central. A qubit can be measured in different bases, analogous to asking different questions about its state. If you precisely measure a qubit in the zero-one basis and find zero, you have destroyed information about its state in other bases. You cannot then measure it in a different basis and expect consistent results.
This matters profoundly for Quantum Computing. Computation happens in the probabilistic amplitude space where superposition and interference operate. Successful algorithms preserve useful quantum structure until the final step, when measurement collapses the state. The algorithm must ensure that the interference has arranged amplitudes so that measurement yields the correct answer with high probability.
Quantum error correction must protect quantum information without measuring it, since measurement would destroy the superposition. Instead, error correction encodes information redundantly across multiple qubits and performs carefully designed operations that detect and fix errors without revealing the protected information directly.
Quantum Computing and Measurement Principles
| Measurement Aspect | Impact on Quantum Computing |
|---|---|
| State Collapse | Transforms superposed qubits into definite classical outcomes ending computation |
| Basis Dependence | Different measurement choices extract different information from quantum states |
| Irreversibility | Cannot undo measurement making it one-way transition from quantum to classical |
| Probabilistic Outcomes | Results follow quantum probability distributions not deterministic predictions |
| Observer Effect | Measurement inevitably disturbs system preventing passive information extraction |
| Complementarity | Precise measurement in one basis destroys information about complementary bases |
6. Quantum Computing and Error Correction: Preserving Fragile Quantum Information
Qubits are delicate. A stray photon, a vibration, a fluctuation in electromagnetic fields, any of these can disturb a qubit’s quantum state. This process, called decoherence, converts quantum information into classical noise. For early quantum computers, qubits maintain their quantum properties for mere microseconds or milliseconds before decoherence destroys them.
Classical computers also experience errors from noise, but they handle them differently. Classical bits are stable. Even if the voltage fluctuates slightly, the system can still distinguish zero from one reliably. Classical error correction simply copies bits multiple times. If three copies say zero and one says one, the majority probably indicates the true value.
Quantum Computing cannot copy qubits. The no-cloning theorem proves that unknown quantum states cannot be duplicated perfectly. This seems to rule out redundancy-based error correction. Yet quantum error correction is possible through clever encoding.
Instead of copying a single qubit, quantum error correction spreads its information across multiple physical qubits, forming one logical qubit. The Shor code, among the first quantum error correction schemes, protects one logical qubit using nine physical qubits. The information is encoded in quantum correlations between these qubits rather than in any individual qubit’s state.
When errors occur, they disturb the correlations in detectable ways. The system can measure these error syndromes without learning the logical qubit’s state itself, preserving the quantum information. Based on the syndrome, corrective operations restore the original correlations. This process protects against decoherence while maintaining superposition and entanglement.
The catch is overhead. Protecting each logical qubit requires many physical qubits. Current estimates suggest thousands or millions of physical qubits might be needed for each reliable logical qubit in a fault-tolerant quantum computer. This requirement drives efforts to improve qubit quality and develop better error correction codes.
Quantum Computing Error Correction Challenges
| Error Source | Correction Strategy |
|---|---|
| Decoherence | Encodes logical qubits across multiple physical qubits with syndrome measurement |
| Gate Errors | Uses fault-tolerant protocols preventing error propagation during operations |
| Measurement Errors | Employs repeated measurements and statistical analysis for reliable readout |
| Crosstalk | Minimizes unwanted interactions through careful qubit placement and control |
| Control Noise | Calibrates operations frequently and uses dynamical decoupling sequences |
| Environmental Coupling | Isolates qubits at extreme temperatures with magnetic and electromagnetic shielding |
Conclusion: Building the Future with Quantum Computing Breakthroughs
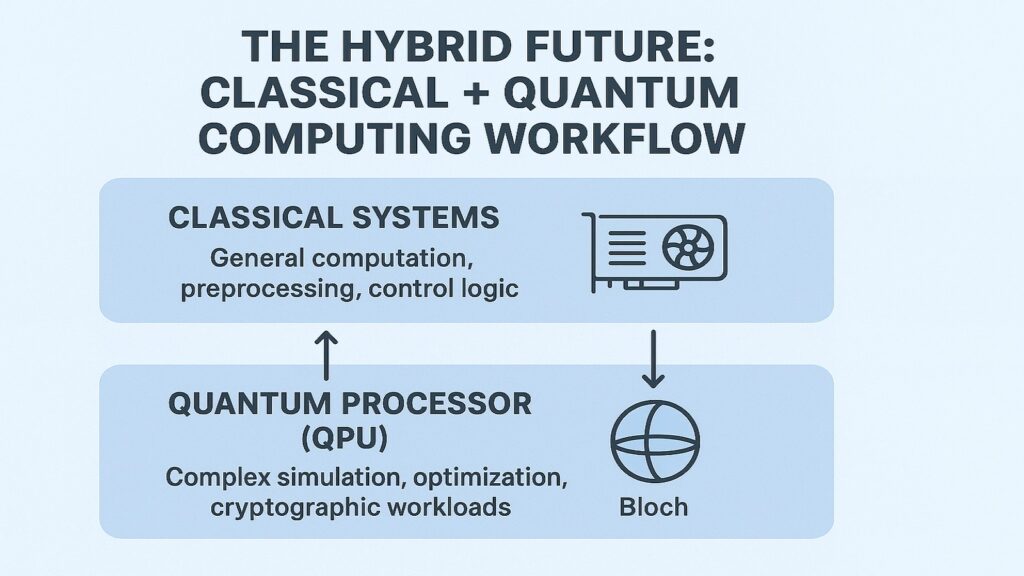
Quantum Computing rests on six interconnected principles. Superposition expands the computational space exponentially. Entanglement coordinates quantum states without classical communication. Interference focuses this expanded space toward solutions. Tunneling explores possibilities beyond barriers. Measurement and uncertainty shape how information transitions from quantum to classical. Error correction protects fragile quantum states long enough for computation to complete.
Together, these concepts create a computing paradigm fundamentally different from classical approaches. The difference is not merely quantitative, not just faster processing of the same operations. It is qualitative, enabling new algorithms that solve certain problems exponentially faster than any classical approach could.
Yet, Quantum Computing does not replace classical computing. Quantum algorithms excel at specific tasks like factoring, database search, quantum simulation, and certain optimization problems. For most everyday computing, classical systems remain superior. They are stable, well-understood, and efficient at tasks like word processing, web browsing, and video playback.
The future likely involves hybrid systems. Classical computers handle routine tasks and orchestrate overall workflows. Quantum computing tackles specialized subtasks where quantum advantage emerges. This partnership already appears in quantum chemistry simulations, where classical computers manage molecular structures while quantum systems compute electronic interactions.
Challenges remain substantial. Building reliable logical qubits requires orders of magnitude more physical qubits than current systems contain. Developing quantum algorithms for practical problems needs continued mathematical innovation. Integrating quantum processors into existing computing infrastructure demands new architectures and software tools.
Despite obstacles, progress continues steadily. Companies and research institutions worldwide invest billions in quantum computing and quantum technology. Multiple competing qubit technologies show promise. Theoretical advances reveal new algorithms and applications. The quantum workforce grows as universities establish quantum education programs.
Quantum Computing will not suddenly revolutionize all computing overnight. Instead, it will gradually expand into niches where quantum effects provide clear advantages. Drug discovery might accelerate through better molecular simulations. Logistics companies could optimize supply chains more efficiently. Cryptography will evolve to address quantum threats while harnessing quantum security.
Quantum Computing Future Development Areas
| Development Focus | Expected Innovation Impact |
|---|---|
| Hardware Scaling | Increasing physical qubit counts toward millions for fault-tolerant systems |
| Algorithm Design | Creating new quantum algorithms for practical optimization and simulation |
| Error Mitigation | Developing techniques to extract value from noisy intermediate-scale devices |
| Software Tools | Building programming frameworks accessible to domain experts beyond physicists |
| Application Discovery | Identifying real-world problems where quantum advantage becomes practical |
| Integration Architecture | Designing hybrid classical-quantum systems for seamless workflow incorporation |
Quantum revolution unfolds slowly but inexorably. Each advance builds on decades of physics, mathematics, and engineering. Understanding the core principles, superposition, entanglement, interference, tunneling, measurement, and error correction, provides insight into both the promise and challenges ahead. Quantum Computing emerges not from hype or speculation but from fundamental physics validated through rigorous experiment. As technology matures, these six powerful concepts will drive genuine innovation across science, industry, and society.
Read More Tech Articles
- Machine Learning in AI: 6 Powerful Ways AI Learns
- Artificial Intelligence: 8 Powerful Insights You Must Know
- Hisense Smart TVs: 6 Stunning Picks for 2025
- Xiaomi Smart TVs 2025: 6 Stunning Picks You Will Love
- Suunto Fitness Trackers 2025: Top 6 Brilliant Picks Revealed
- Xiaomi Smart Bands: Discover 6 Best Picks for 2025
- Whoop Fitness Bands In 2025: Explore 6 Brilliant Picks
- 8 Powerful Smart Devices To Brighten Your Life
- Huawei MatePad: Top 6 2025 Picks for Ultimate Power Users